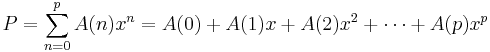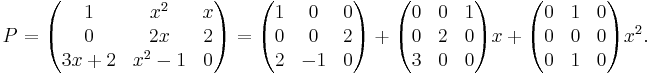Polynomial matrix

Not to be confused with matrix polynomial.

In mathematics, a polynomial matrix or sometimes matrix polynomial is a matrix whose elements are univariate or multivariate polynomials. A λ-matrix is a matrix whose elements are polynomials in λ.

A univariate polynomial matrix P of degree p is defined as:

$P = \sum_{n=0}^p A(n)x^n = A(0)%2BA(1)x%2BA(2)x^2%2B \cdots %2BA(p)x^p$

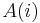where $A(i)$ denotes a matrix of constant coefficients, and 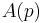$A(p)$ is non-zero. Thus a polynomial matrix is the matrix-equivalent of a polynomial, with each element of the matrix satisfying the definition of a polynomial of degree p.

An example 3×3 polynomial matrix, degree 2:

$P=\begin{pmatrix} 1 & x^2 & x \\ 0 & 2x & 2 \\ 3x%2B2 & x^2-1 & 0 \end{pmatrix} =\begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 2 \\ 2 & -1 & 0 \end{pmatrix} %2B\begin{pmatrix} 0 & 0 & 1 \\ 0 & 2 & 0 \\ 3 & 0 & 0 \end{pmatrix}x%2B\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}x^2.$

We can express this by saying that for a ring R, the rings $M_n(R[X])$ and $(M_n(R))[X]$ are isomorphic.

Properties

A polynomial matrix over a field with determinant equal to a non-zero element of that field is called unimodular, and has an inverse that is also a polynomial matrix. Note that the only scalar unimodular polynomials are polynomials of degree 0 - nonzero constants, because an inverse of an arbitrary polynomial of higher degree is a rational function.
The roots of a polynomial matrix over the complex numbers are the points in the complex plane where the matrix loses rank.

Note that polynomial matrices are not to be confused with monomial matrices, which are simply matrices with exactly one non-zero entry in each row and column.

If by λ we denote any element of the field over which we constructed the matrix, by I the identity matrix, and we let A be a polynomial matrix, then the matrix λI-A is the characteristic matrix of the matrix A. Its determinant, |λI-A| is the characteristic polynomial of the matrix A.

References

E.V.Krishnamurthy, Error-free Polynomial Matrix computations, Springer Verlag, New York, 1985